从暴力破解到动态规划解答题目连续子数组的最大和

Code Comments

梳理一下自己从暴力破解到动态规划的整个过程，希望可以帮到大家。

  1. 解此题，最容易想到的思路就是暴力破解，但是时间复杂度至少会是$O(n^2)$，有两种写法：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    // 时间复杂度：O(n^3)
    class Solution {
        public int maxSubArray(int[] nums) {
            int max = Integer.MIN_VALUE;
            for(int i = 0;i < nums.length;i++){
                for(int j = i;j < nums.length;j++){
                    // 计算sum(i,j)
                    int sum = 0;
                    for(int k = i;k<j;k++)
                        sum+=nums[k];
                    if(sum > max)
                        max = sum;
                }
            }
            return max;
        }
    }
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    // 时间复杂度：O(n^2)
    class Solution {
        public int maxSubArray(int[] nums) {
            int max = Integer.MIN_VALUE;
            for(int i = 0;i < nums.length;i++){
                int sum = 0;
                for(int j = i;j < nums.length;j++){
                    //sum(i,j)=sum(i,j-1)+nums[j]
                    sum += nums[j];
                    if(sum > max)
                        max = sum;
                }
            }
            return max;
        }
    }

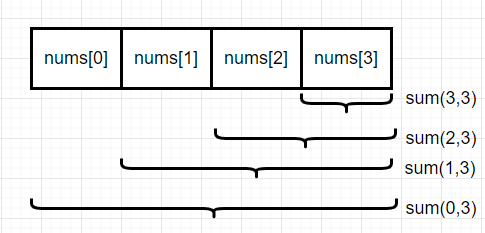
  2. 无论那种暴力破解，过程中需要计算的子数组一定如下所列，其中$sum(i,j)$代表计算从$nums[i]$到$nums[j]$的元素之和，我们要找到最大的 $sum(i,j)$。
sum(0,0)
sum(0,1) sum(1,1)
sum(0,2) sum(1,2) sum(2,2)
sum(0,3) sum(1,3) sum(2,3) sum(3,3)
….. … … ….

  1. 假如我们要以$O(n)$的时间复杂度优化算法，就需要进一步压缩计算。

    观察上边这个表格，如果我们每次能在最右侧得到该行的最大值，然后再求这么多最大值的最大值，岂不就能在$O(n)$内计算出结果？

行最大值
sum(0,0) dp[0]
sum(0,1) sum(1,1) dp[1]
sum(0,2) sum(1,2) sum(2,2) dp[2]
sum(0,3) sum(1,3) sum(2,3) sum(3,3) dp[3]
….. … … …. dp[j]

表格每一行的子数组都是以某一值结尾，所以我们设$dp[j]$为以$j$ 结尾的子数组的最大值，如上面表格所示。$dp[j]$的最大值就是我们要的结果。

  1. 如何计算$dp[j]$呢？

    以$sum(0,3) 、 sum(1,3) 、 sum(2,3) 、 sum(3,3)$为例，我们思考一下怎么求四者最大值。

    image.png

    可以看到，四者同时包含$nums[3]$，比较四者哪个更大，其实就是比较$0、nums[2]、nums[1]+nums[2]、nums[0]+nums[1]+nums[2]$四者谁大谁小。

    有没有发现规律？$nums[2]、nums[1]+nums[2]、nums[0]+nums[1]+nums[2]$这三者的最大值恰好就是dp[2]。所以，如果dp[2]>0，dp[3]=dp[2]+nums[3]，否则，dp[3] = 0 + nums[3]。用公式表示就是：

  2. 最后一步，就是对上面所有的$dp[j]$求最大值。所以，动态规划的代码如下：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    class Solution {
        public int maxSubArray(int[] nums) {
            int[] dp = new int[nums.length];
            dp[0]=nums[0];
            for(int j = 1;j<nums.length;j++){
                if(dp[j-1]>0){
                    dp[j] = dp[j-1]+nums[j];
                }else{
                    dp[j] = nums[j];
                }
            }
            int max = Integer.MIN_VALUE;
            for(int i = 0;i<dp.length;i++){
                if(dp[i]>max)
                    max = dp[i];
            }
            return max;
        }
    }

    最基础的动态规划做法到这就结束了，关于动态规划的再优化，本文不再赘述。

KarakaruaDeveloper

学无止境